


Next: Regular Expressions
Up: Non-Standard Language Constructs of
Previous: Non-Standard Language Constructs of
XASM provides the possibility to define and use constructor
terms. The concept of constructor terms can be mapped to the ASM
core language as follows: According to [16] each of the
function names contained in the vocabulary V of an ASM may be marked
as relational or static, or both. In addition, we allow
static functions to be marked as constructive. Let 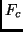 be the
set containing all functions in V marked as constructive,
be the
set containing all functions in V marked as constructive,
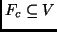 . Let
. Let 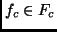 , arity of
, arity of 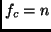 , then the
following conditions hold for all states A of the ASM:
, then the
following conditions hold for all states A of the ASM:
- (i)
-
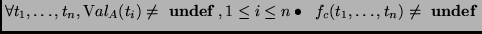
- (ii)
-
![$\begin{array}[t]{@{}l}
\forall g_c\in F_c, \mbox{arity of $g_c$ is $m$}; t_1...
...pace*{2mm}\wedge \mbox Val_A(t_i) = \mbox Val_A(s_i), 1\leq i\leq n
\end{array}$](img31.png)
where
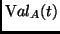 stands for the evaluation of term t in state A
of the ASM. Informally speaking that means that each constructive
function is (i) defined at all locations and that (ii) the content of
each location is a unique element of the superuniverse w.r.t. the set
of locations of all constructive functions. If
stands for the evaluation of term t in state A
of the ASM. Informally speaking that means that each constructive
function is (i) defined at all locations and that (ii) the content of
each location is a unique element of the superuniverse w.r.t. the set
of locations of all constructive functions. If 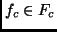 , then
, then
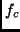 is called a constructor, and the terms
is called a constructor, and the terms
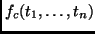 are called constructor terms.
In XASM, the declaration of a constructor is part of the function
declarations, for example
are called constructor terms.
In XASM, the declaration of a constructor is part of the function
declarations, for example
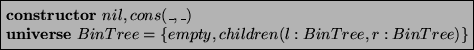
introduces the constructors nil, cons, empty, and children,
where terms constructed using the latter two constructors are elements
of the universe BinTree.
XASM also provides pattern matching functionality like it is used in
many other languages. Syntactically, pattern matching terms are used
as condition terms in conditionals, e. g.:
![[*]](file:/usr/lib/latex2html/icons/footnote.png)

There are three kinds of pre-defined, commonly-used constructors in
XASM: sets, sequences, and tuples. These constructors are specified
using their usual representation:
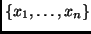 for sets,
for sets,
![$[x_1,\ldots,x_n]$](img38.png) for sequence, and
for sequence, and
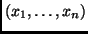 for
n-tuples. For sequences, the notation
for
n-tuples. For sequences, the notation ![$[H\vert T]$](img40.png) can be used in pattern
matching terms for accessing head and tail of a sequence.
can be used in pattern
matching terms for accessing head and tail of a sequence.



Next: Regular Expressions
Up: Non-Standard Language Constructs of
Previous: Non-Standard Language Constructs of
Philipp Kutter
2002-03-18
![$\begin{array}[t]{@{}l}
\forall g_c\in F_c, \mbox{arity of $g_c$ is $m$}; t_1...
...pace*{2mm}\wedge \mbox Val_A(t_i) = \mbox Val_A(s_i), 1\leq i\leq n
\end{array}$](img31.png)
![$\begin{array}[t]{@{}l}
\forall g_c\in F_c, \mbox{arity of $g_c$ is $m$}; t_1...
...pace*{2mm}\wedge \mbox Val_A(t_i) = \mbox Val_A(s_i), 1\leq i\leq n
\end{array}$](img31.png)
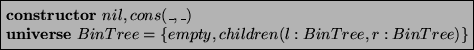
![]()

![]() for sets,
for sets,
![]() for sequence, and
for sequence, and
![]() for
n-tuples. For sequences, the notation
for
n-tuples. For sequences, the notation ![]() can be used in pattern
matching terms for accessing head and tail of a sequence.
can be used in pattern
matching terms for accessing head and tail of a sequence.